Abstract
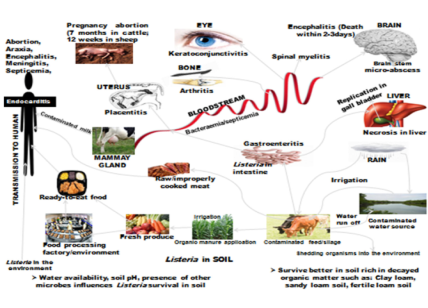
Human Listeriosis is a fatal zoonotic foodborne disease which is caused by the consumption of contaminated food products. In this thesis, four mathematical models which incorporate; cross-contamination of ready-to-eat food products, awareness programs and optimal control were used to model Listeriosis disease transmission dynamics. Food contamination threshold, Rwf , food generation number Rf and the model equilibria namely; disease-free, Listeria-free and endemic equilibria were determined. Using Routh-Hurwitz criterion we established the local stability of the equilibrium points based on the Rw f for the first model and Rf for the rest of the models. Our findings show that for each of the models the disease-free equilibria were locally asymptotically stable for Rwf and Rf less than unity while the Listeria and endemic equilibria were locally asymptotically stable whenever food contamination is greater than unity. Numerical simulations and Latin-Hyper Cube sampling sensitivity analysis of each model were carried out to determine the most influential parameters driving Listeriosis epidemic. Also, Pontryagain Maximum Principle was used to formulate an optimal control problem. Results from the numerical simulations suggest that an increase in contaminated food removal rate, decreasing rate of food contamination, a constant implementation of awareness programs, joint implementation of effects of media campaigns, treatment and removal of contaminated food products is essential in the control and possible eradication of the disease. The results obtained through mathematical analyses and the numerical simulations have a pivotal role in the control and management of the disease in the event of any Listeriosis outbreak.